Estadísticas descriptivas y visualización en R
By Javier Tamayo-Leiva
- 18 minutes read - 3794 wordsTable of Content
- Introducción
- Cargar tus datos en R
- Estadística descriptiva con {stat} en R
- Grafica tus datos con {ggplot2}
- Complementa tus análisis con {ggpubr}
- Gráfico final
Introducción
He visto con frecuencia que la gente está interesada en aprender R por las visualizaciones que se pueden generar con paquetes como {ggplot2}. Sin embargo, R es un lenguaje de programación, por lo que su potencia no se limita sólo a eso, sino que también es una potente herramienta para el análisis estadístico. Por lo tanto, el objetivo principal de este post es proporcionar herramientas para generar análisis estadísticos descriptivos, y visualizaciones asociadas. Esto nos permitirá explorar mejor nuestros datos en busca de patrones. Para ello, aquí seguirás una guía paso a paso para realizar análisis estadísticos descriptivos y generar visualizaciones de tus datos que te ayuden a entenderlos mejor.
Cargar tus datos en R
R tiene diferentes métodos a la hora de cargar conjuntos de datos, sin embargo con el uso de un IDE (Integrated Development Environment) como RStudio, podemos simplificar mucho este proceso.
Lo primero que tenemos que hacer una vez que hayamos instalado R y RStudio, es instalar la librería {readR} de {tidyverse} para ayudarnos a cargar los datos. Para ello debemos ejecutar el siguiente código en nuestra sesión de R.
# Instalar todos los paquetes de {tidyverse} (Recomendado)
install.packages("tidyverse")
# Instalar solo {readR}
install.packages("readr")¿Cómo cargar mis datos desde RStudio?
Una vez que hayamos instalado nuestros paquetes, lo que tenemos que hacer en RStudio es ir a la pestaña “Environment” y luego hacer clic en el menú desplegable de la pestaña “Import Dataset”. En esta pestaña podremos seleccionar si queremos importar nuestros datos desde un archivo de texto (ej. csv, tsv, etc.) o si queremos hacerlo desde un archivo de Excel (ej. xlsx).
Environment -> Import Dataset -> From text (base), From text (readr), o From Excel
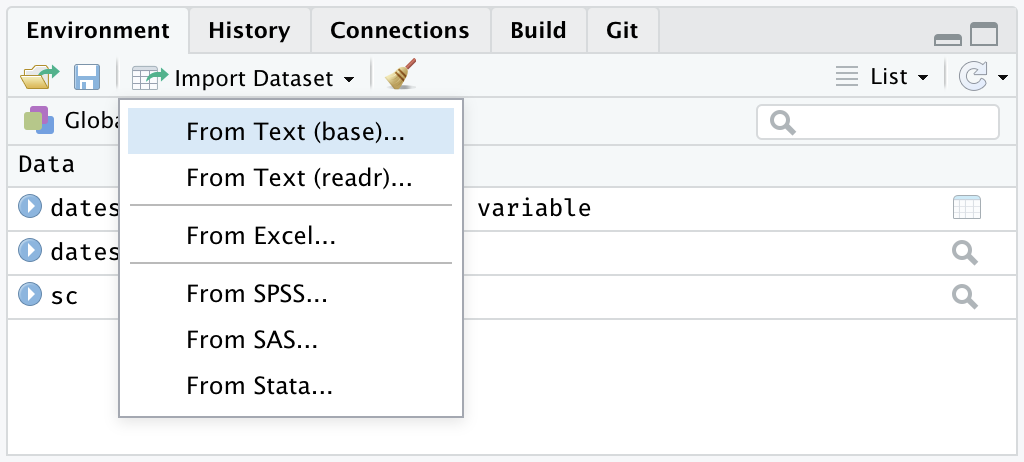
Del mismo modo, la pestaña Import Dataset se puede encontrar buscando la pestaña File directamente en el menú de la parte superior.
File -> Import Dataset -> From text (base), From text (readr), o From Excel
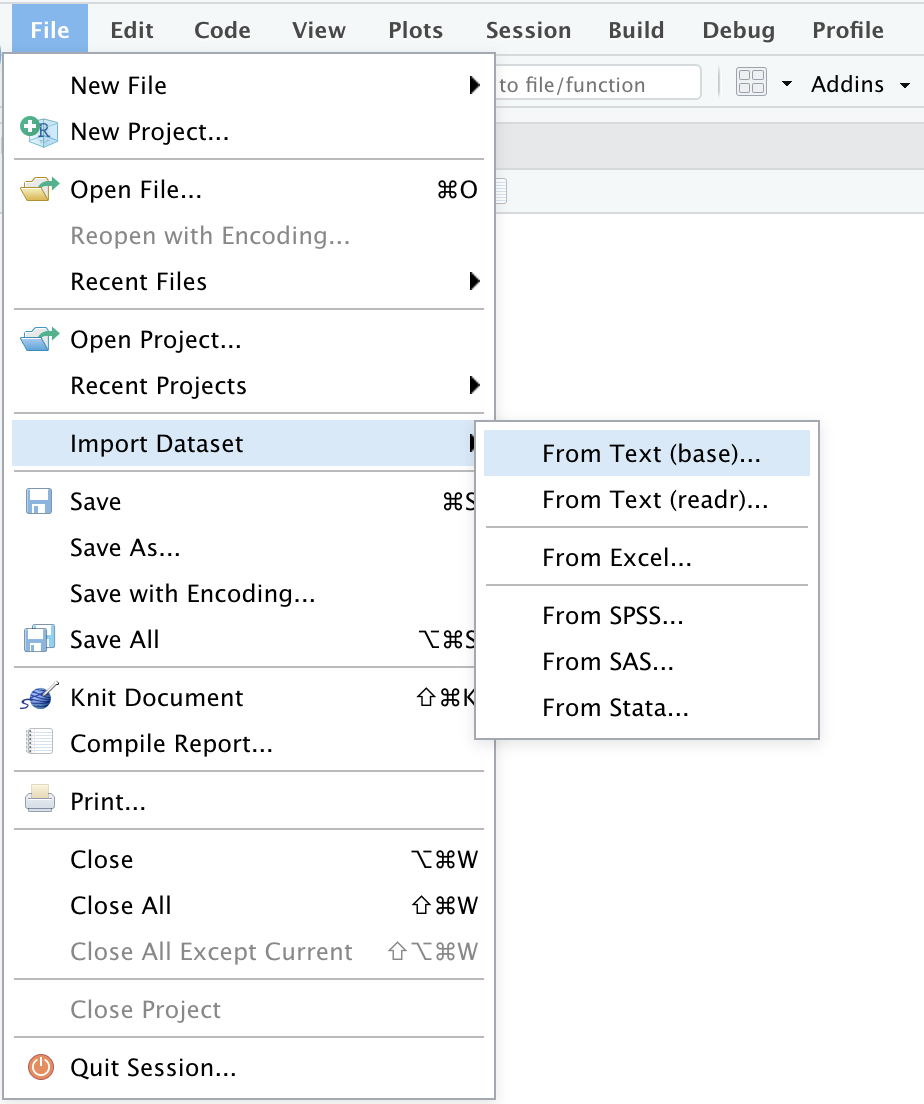
Una vez que hayamos completado estos pasos, se desplegará una ventana en la que podremos revisar nuestros datos de interés y en la que incluso podremos realizar algunas modificaciones de forma manual. Puedes encontrar más detalles sobre los tipos de archivos que puedes subir y las modificaciones que puedes hacer en el artículo original de RStudio que puedes encontrar en el siguiente link.
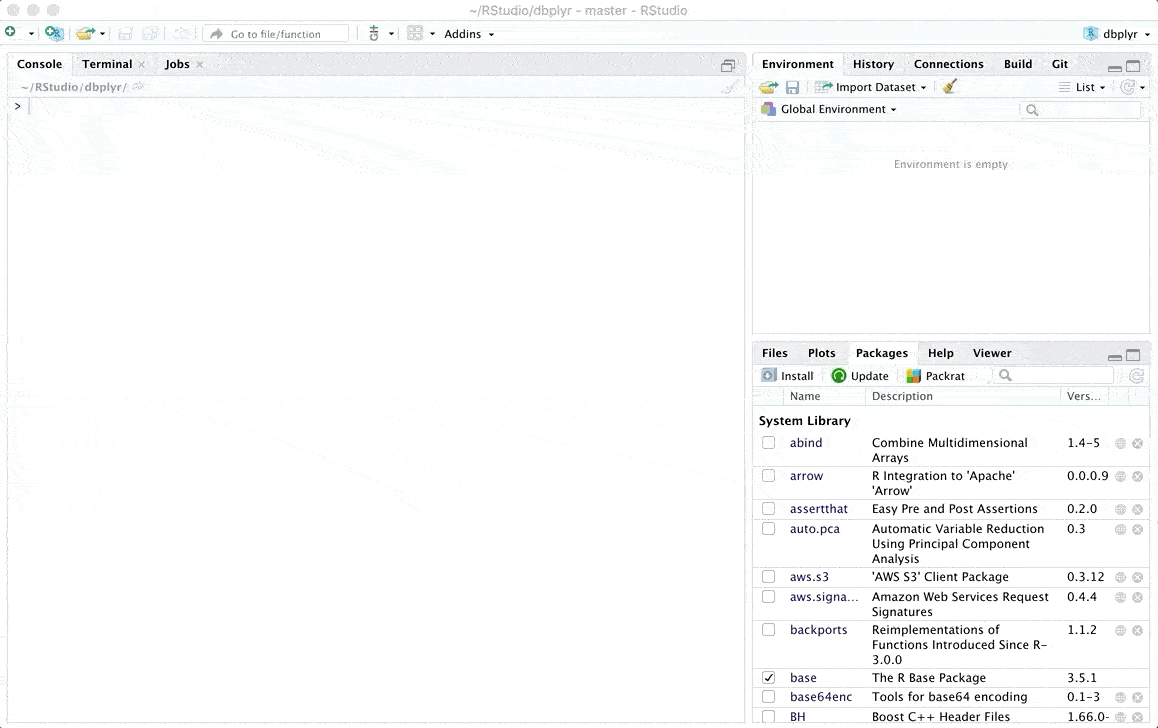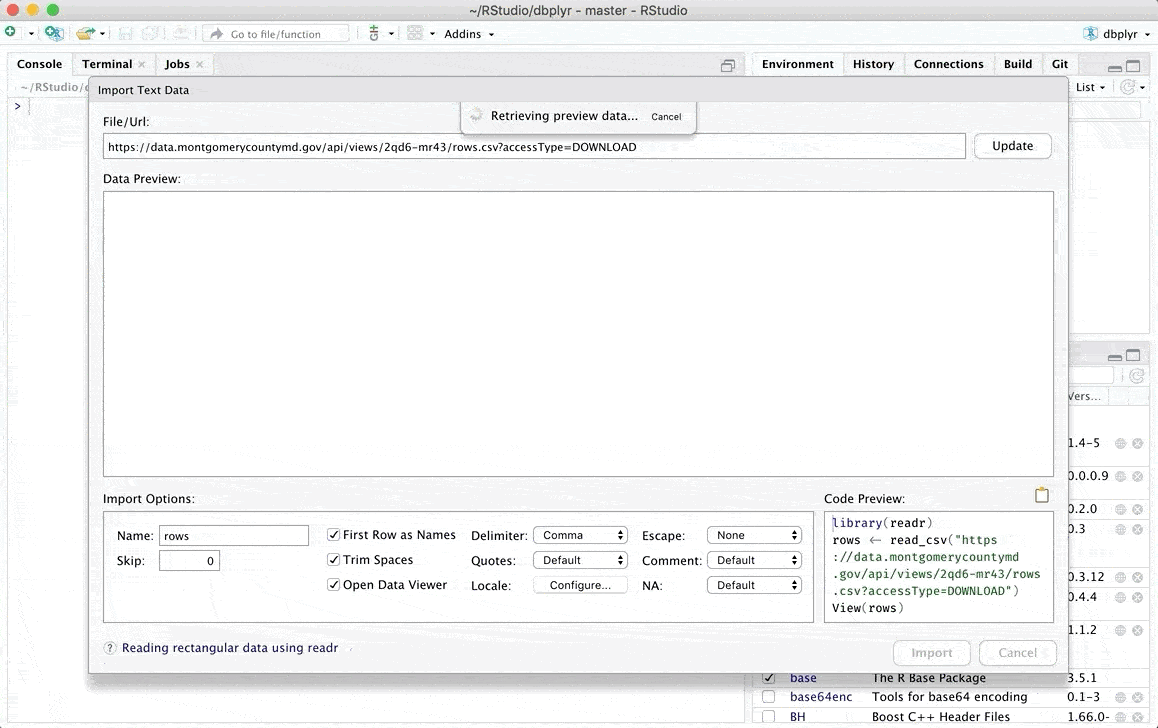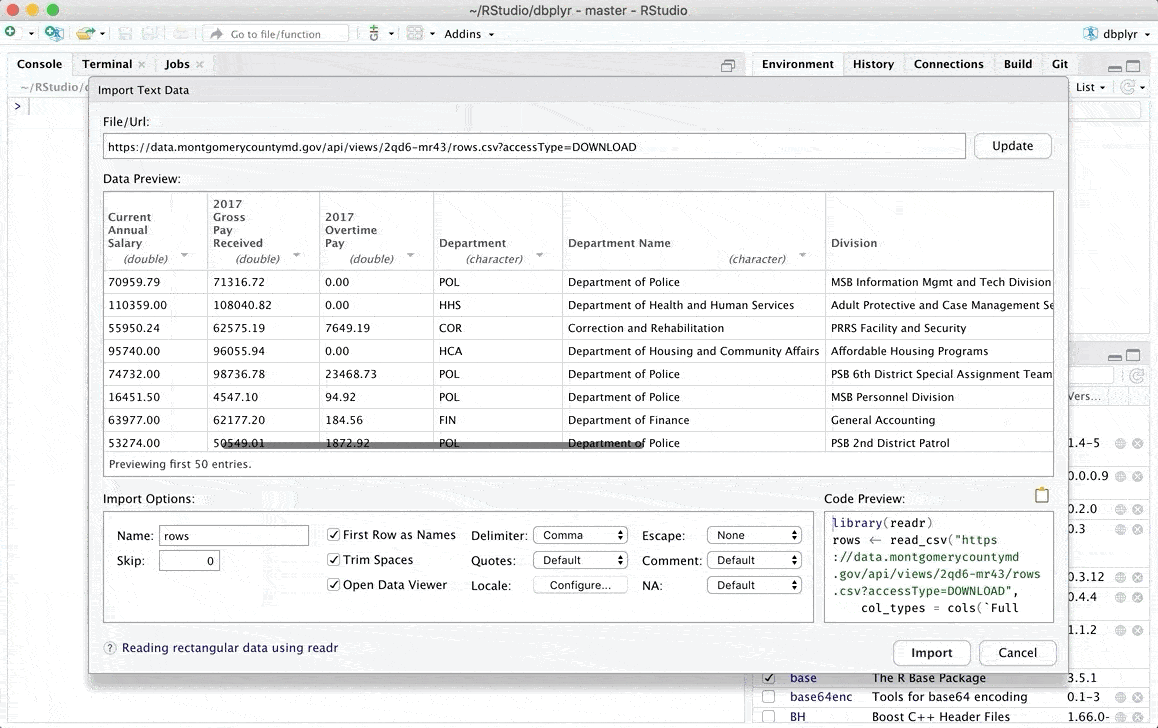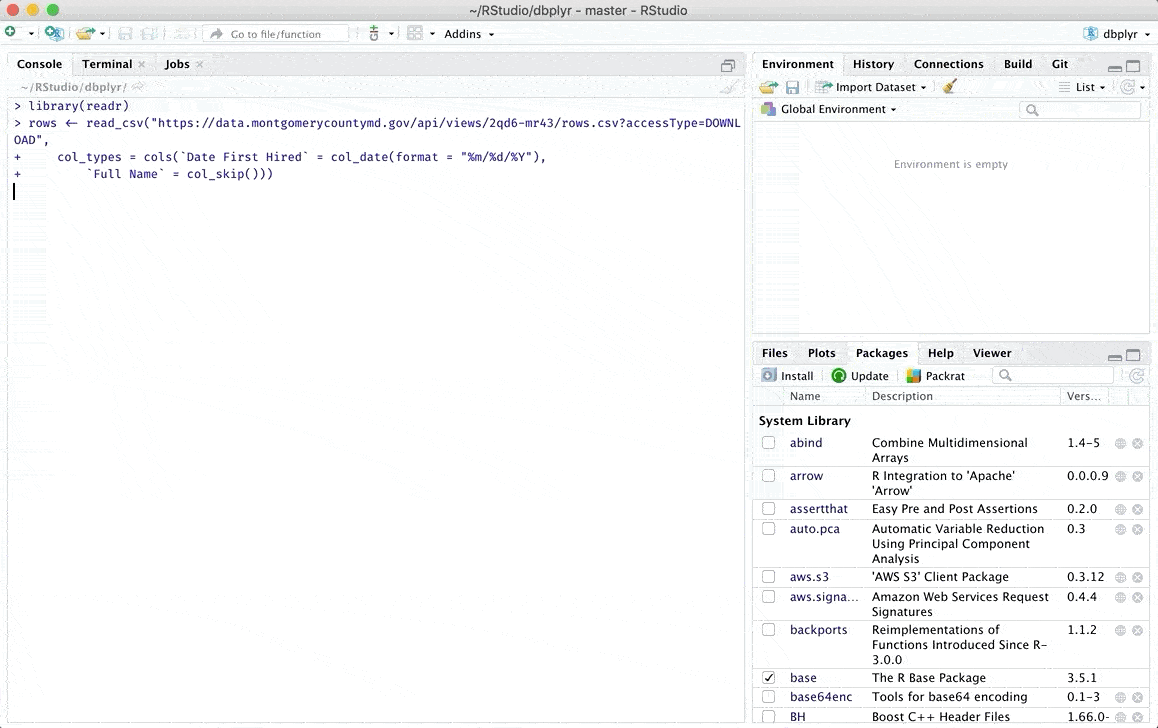
Adicionalmente existen otras opciones para cargar datos en R, si te interesa puedes revisar otra alternativa en uno de mis posts anteriores De la carga de los datos a la visualización en R (fácilmente)
Estadística descriptiva con {stat} en R
{stat} es un paquete de R que se carga por defecto al iniciar la sesión (no es necesario llamar a la librería para utilizarla). Su objetivo es proporcionar herramientas para realizar cálculos estadísticos (desde los más básicos hasta los avanzados), y la y la generación de conjuntos numéricos. Para conocer las funciones que puede realizar el paquete {stat}, puede ejecutar el siguiente código en su sesión de R.
library(help = "stats")Para el ejemplo de hoy utilizaremos el conjunto de datos de los penguins que puedes descargar haciendo clic en el siguiente enlace: penguins.csv
A continuación podemos repasar la estructura del conjunto de datos penguins.
Entre todas las variables, para nuestro análisis seleccionaremos “bill_length_mm” (longitud del pico en milímetros) y “bill_depth_mm” (profundidad del pico en milímetros) porque son variables continuas.
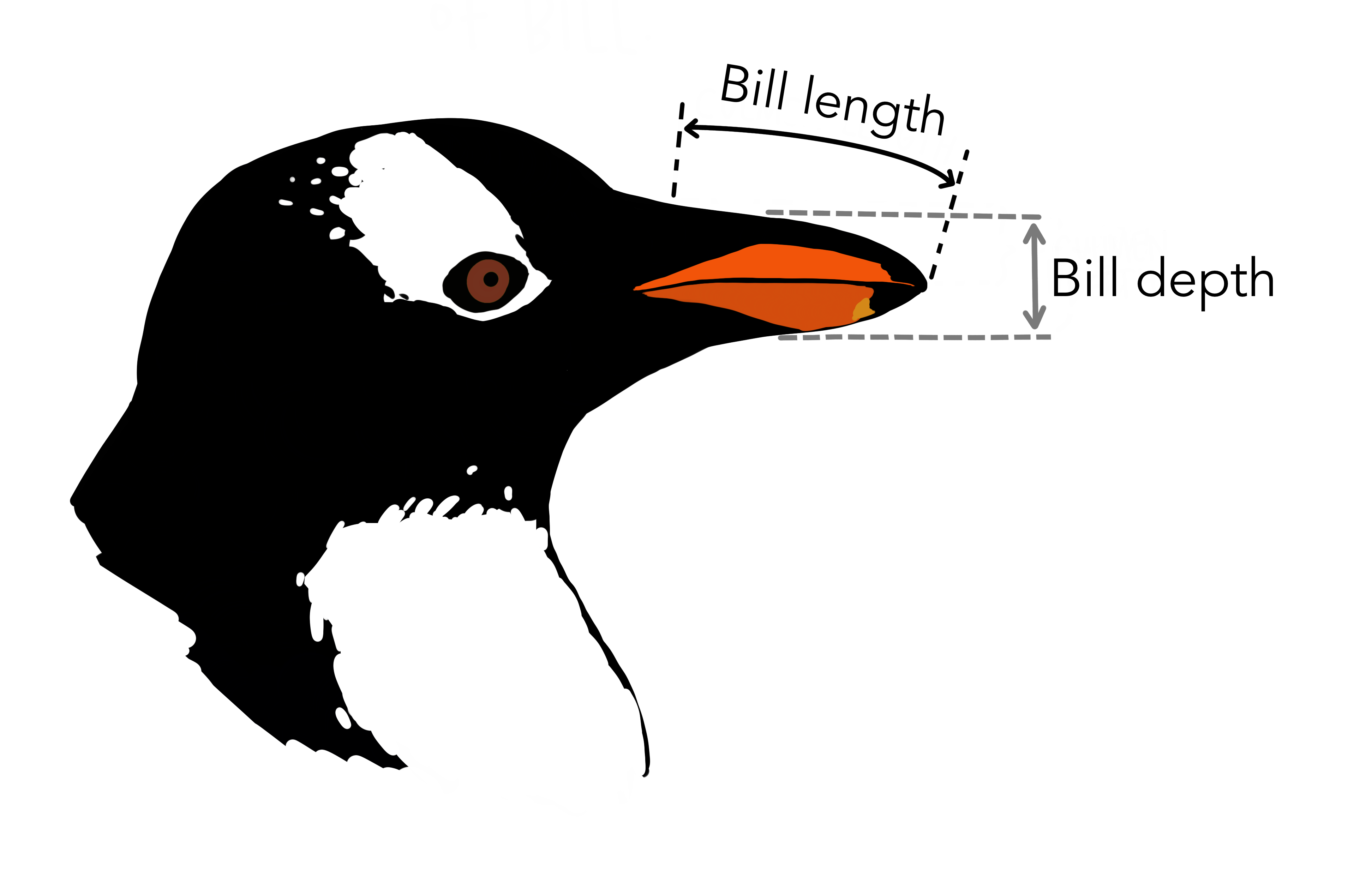
Medidas de tendencia central
El primer y más sencillo análisis corresponde al cálculo de la media (mean). Hay que tener en cuenta que el primer argumento corresponde al conjunto de datos y a la variable que queremos analizar (penguins$bill_length_mm). Nuestro segundo argumento es na.rm = TRUE para eliminar cualquier observación con NA de la variable de interés en el análisis.
mean(penguins$bill_length_mm, na.rm = TRUE)## [1] 43.92193También podemos calcular la mediana (valor que separa el 50% superior del inferior) de la misma manera, sólo tenemos que cambiar la función a median.
median(penguins$bill_length_mm, na.rm = TRUE)## [1] 44.45Medidas de dispersión
Podemos calcular el mínimo (min), el máximo (max) y el rango (range min - max) de una variable continua.
min(penguins$bill_length_mm, na.rm = TRUE)## [1] 32.1max(penguins$bill_length_mm, na.rm = TRUE)## [1] 59.6range(penguins$bill_length_mm, na.rm = TRUE)## [1] 32.1 59.6Podemos calcular los cuantiles (valores que dividen la distribución en n intervalos regulares) de una variable continua. En este ejemplo utilizaremos los cuartiles 0,25 (Q1), 0,5 (Q2) y 0,75 (Q3).
quantile(penguins$bill_length_mm, prob = c(0.25, 0.5, 0.75), na.rm = TRUE)## 25% 50% 75%
## 39.225 44.450 48.500Del mismo modo, podemos calcular medidas de dispersión para nuestros datos, como la varianza o la desviación estándar.
var(penguins$bill_length_mm, na.rm = TRUE)## [1] 29.80705sd(penguins$bill_length_mm, na.rm = TRUE)## [1] 5.459584Por último, {stat} tiene una función que nos permite calcular todas estas métricas (media, mediana, cuartiles 0,25 (Q1) y 0,75 (Q3), mínimo, máximo, NA’s) sobre cada variable presente en un conjunto de datos. La función se llama summary y se utiliza como a continuación.
summary(penguins$bill_length_mm)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 32.10 39.23 44.45 43.92 48.50 59.60 2Si quieres calcularlo sobre todas las variables (continuas y discretas) del conjunto de datos, utiliza el siguiente código.
summary(penguins)Medidas de distribución
Con {stat} también podemos analizar la distribución de nuestros datos con medidas que nos permiten comprobar la normalidad y la homocedasticidad.
Pueba de normalidad Shapiro-Wilk:
Se usa para probar la normalidad en la distribución de los datos para una variable. Se puede ocupar en grupos con no más de 5000 observaciones (N < 5000).
Hipotesis
- H0 = La variable muestra una distribución normal
- H1 = La variable no muestra una distribución normal
Interpretación
- p-value > alfa: No rechazar H0 (normal)
- p-value < alfa: Rechazar H0 (no normal)
Nota
alfa hipotético 5% (0,05)
shapiro.test(penguins$bill_length_mm)##
## Shapiro-Wilk normality test
##
## data: penguins$bill_length_mm
## W = 0.97485, p-value = 1.12e-05Pueba de homocedasticidad Bartlett’s test
Se usa para probar la homogeneidad de varianza (homocedasticidad) en k grupos de muestras, donde k puede ser mayor a dos. Está adaptado para datos distribuidos normalmente.
Hipotesis
- H0 = Los grupos muestra homocedasticidad
- H1 = Los grupos (al menos 2) no muestra homocedasticidad.
Interpretación
- p-value > alfa: No rechazar H0 (homocedasticidad)
- p-value < alfa: Rechazar H0 (no homocedasticidad)
# Una variable independiente
bartlett.test(bill_length_mm ~ sex, data = penguins)##
## Bartlett test of homogeneity of variances
##
## data: bill_length_mm by sex
## Bartlett's K-squared = 1.3429, df = 1, p-value = 0.2465# Múltiples variables independientes
bartlett.test(bill_length_mm ~ interaction(sex,species), data = penguins)##
## Bartlett test of homogeneity of variances
##
## data: bill_length_mm by interaction(sex, species)
## Bartlett's K-squared = 22.178, df = 5, p-value = 0.0004843Pueba de homocedasticidad Fligner-Killeen test
Para probar la homocedasticidad en k grupos de muestras, donde k puede ser mayor que dos. Más robusto frente a las desviaciones de la normalidad o cuando hay problemas relacionados con los valores atípicos (outliers).
Hipotesis
- H0 = Los grupos muestra homocedasticidad
- H1 = Los grupos (al menos 2) no muestra homocedasticidad
Interpretación
- p-value > alfa: No rechazar H0 (homocedasticidad)
- p-value < alfa: Rechazar H0 (no homocedasticidad)
# Una variable independiente
fligner.test(bill_length_mm ~ sex, data = penguins)##
## Fligner-Killeen test of homogeneity of variances
##
## data: bill_length_mm by sex
## Fligner-Killeen:med chi-squared = 3.0297, df = 1, p-value = 0.08175# Múltiples variables independientes
fligner.test(bill_length_mm ~ interaction(sex,species), data = penguins)##
## Fligner-Killeen test of homogeneity of variances
##
## data: bill_length_mm by interaction(sex, species)
## Fligner-Killeen:med chi-squared = 5.9733, df = 5, p-value = 0.3088Análisis de varianza
Son un conjunto de análisis que permiten examinar si las medias de los grupos (poblaciones, muestras) difieren entre sí. Hay métodos que se diferencian por el número de grupos que pueden comparar. Además, hay métodos paramétricos (que exigen que se cumplan los supuestos) y métodos no paramétricos (que no exigen que se cumplan todos los supuestos) que son más robustos ante el incumplimiento de algunos de los tres supuestos de los datos.
Supuestos
- Independencia (las observaciones son independientes entre sí)
- Normalidad (los elementos de una muestra tienen una distribución normal)
- Homocedasticidad (la varianza de los grupos son similares)
ANOVA (una vía)
ANOVA es una técnica estadística que se utiliza para comparar las medias de dos o más grupos. ANOVA requiere que los grupos cumplan los 3 supuestos.
Importante!
Es necesario notar que ninguna de las variables continuas de nuestro conjunto de datos de penguins tiene una distribución normal, por lo que en este ejemplo utilizaremos la variable bill_length_mm sólo con fines demostrativos, y teniendo en cuenta que el resultado obtenido no es fiable.
peng.aov <- aov(bill_length_mm ~ species, data = penguins)
summary(peng.aov)## Df Sum Sq Mean Sq F value Pr(>F)
## species 2 7194 3597 410.6 <2e-16 ***
## Residuals 339 2970 9
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 2 observations deleted due to missingnessPost-Hoc test para ANOVA
Tukey’s HSD (honestly significant difference) test
TukeyHSD(peng.aov)## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = bill_length_mm ~ species, data = penguins)
##
## $species
## diff lwr upr p adj
## Chinstrap-Adelie 10.042433 9.024859 11.0600064 0.0000000
## Gentoo-Adelie 8.713487 7.867194 9.5597807 0.0000000
## Gentoo-Chinstrap -1.328945 -2.381868 -0.2760231 0.0088993ANOVA (dos vías)
El ANOVA de dos vías nos permite analizar la varianza de la media entre grupos cuando hay interacción entre dos variables categóricas e independientes diferentes.
peng.aov2 <- aov(bill_length_mm ~ species*sex, data = penguins)
summary(peng.aov2)## Df Sum Sq Mean Sq F value Pr(>F)
## species 2 7015 3508 654.189 <2e-16 ***
## sex 1 1136 1136 211.807 <2e-16 ***
## species:sex 2 24 12 2.284 0.103
## Residuals 327 1753 5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 11 observations deleted due to missingnessTukeyHSD(peng.aov2)## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = bill_length_mm ~ species * sex, data = penguins)
##
## $species
## diff lwr upr p adj
## Chinstrap-Adelie 10.009851 9.209424 10.8102782 0.0000000
## Gentoo-Adelie 8.744095 8.070779 9.4174106 0.0000000
## Gentoo-Chinstrap -1.265756 -2.094535 -0.4369773 0.0010847
##
## $sex
## diff lwr upr p adj
## MALE-FEMALE 3.693368 3.194089 4.192646 0
##
## $`species:sex`
## diff lwr upr p adj
## Chinstrap:FEMALE-Adelie:FEMALE 9.315995 7.937732 10.6942588 0.0000000
## Gentoo:FEMALE-Adelie:FEMALE 8.306259 7.138639 9.4738788 0.0000000
## Adelie:MALE-Adelie:FEMALE 3.132877 2.034137 4.2316165 0.0000000
## Chinstrap:MALE-Adelie:FEMALE 13.836583 12.458320 15.2148470 0.0000000
## Gentoo:MALE-Adelie:FEMALE 12.216236 11.064727 13.3677453 0.0000000
## Gentoo:FEMALE-Chinstrap:FEMALE -1.009736 -2.443514 0.4240412 0.3338130
## Adelie:MALE-Chinstrap:FEMALE -6.183118 -7.561382 -4.8048548 0.0000000
## Chinstrap:MALE-Chinstrap:FEMALE 4.520588 2.910622 6.1305547 0.0000000
## Gentoo:MALE-Chinstrap:FEMALE 2.900241 1.479553 4.3209291 0.0000002
## Adelie:MALE-Gentoo:FEMALE -5.173382 -6.341002 -4.0057622 0.0000000
## Chinstrap:MALE-Gentoo:FEMALE 5.530325 4.096547 6.9641020 0.0000000
## Gentoo:MALE-Gentoo:FEMALE 3.909977 2.692570 5.1273846 0.0000000
## Chinstrap:MALE-Adelie:MALE 10.703707 9.325443 12.0819703 0.0000000
## Gentoo:MALE-Adelie:MALE 9.083360 7.931851 10.2348686 0.0000000
## Gentoo:MALE-Chinstrap:MALE -1.620347 -3.041035 -0.1996591 0.0149963Kruskal-Wallis
La prueba de Kruskal-Wallis es una prueba estadística y no paramétrica (no asume la normalidad de los datos) que se utiliza para comparar las medias de dos o más grupos. Es similar al ANOVA pero con datos por categorías.
kruskal.test(bill_length_mm ~ species, data = penguins)##
## Kruskal-Wallis rank sum test
##
## data: bill_length_mm by species
## Kruskal-Wallis chi-squared = 244.14, df = 2, p-value < 2.2e-16Post-Hoc test para Kruskal-Wallis
Mann–Whitney–Wilcoxon o Wilcoxon rank-sum test
pairwise.wilcox.test(penguins$bill_length_mm, penguins$species, p.adjust.method="fdr")##
## Pairwise comparisons using Wilcoxon rank sum test with continuity correction
##
## data: penguins$bill_length_mm and penguins$species
##
## Adelie Chinstrap
## Chinstrap <2e-16 -
## Gentoo <2e-16 0.0018
##
## P value adjustment method: fdrGrafica tus datos con {ggplot2}
{ggplot2} Es un paquete de R orientado a la visualización de datos. Fue creado por Hadley Wickham en 2005 y se basa en la “Grammar of Graphics” de Leland Wilkinson. Brevemente, la “Grammar of Graphics” es un enfoque general de la visualización de datos, en el que un gráfico se separa en componentes semánticos como escalas y capas.
Así que, si aún no hemos instalado {ggplot2}, lo que tenemos que hacer en RStudio es instalar y cargar la librería {ggplot2} con el siguiente código:
- Instalar la librería de paquetes Tidyverse completa (recomendado)
# Instalar desde CRAN (The Comprehensive R Archive Network)
install.packages("tidyverse")
# Cargar las librerías
library(tidyverse)- Instalar solo la librería {ggplot2}
# Instalar desde CRAN
install.packages("ggplot2")
# Cargar la librería
library(ggplot2)Gráfico básico
El primer gráfico que crearemos corresponde a un gráfico de densidad (seleccionado a través del objeto geom_density). Para ello sólo necesitaremos una variable continua (x = bill_length_mm), ya que ggplot2 generará el resto de la información necesaria a través de transformaciones y cálculos estadísticos. De esta forma no tendrás que generar ninguna manipulación a tus datos antes de graficarlos.
Densiplot
ggplot(data = penguins,
mapping = aes(x = bill_length_mm)) +
geom_density()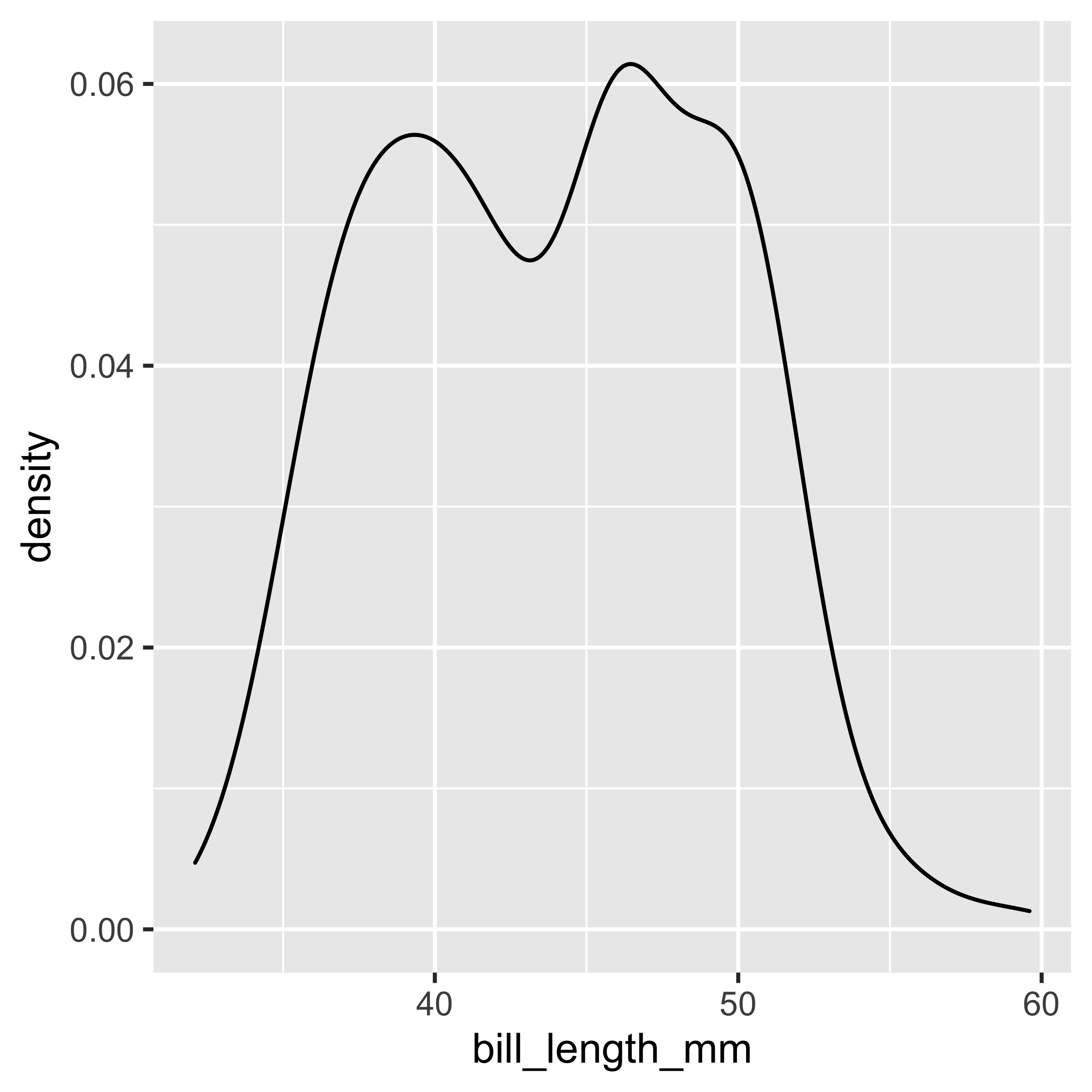
El densiplot calcula y traza la estimación de la densidad de los datos (es una versión suavizada del histograma). El densiplot nos permite ver la distribución de nuestros datos, y el área bajo la curva del densiplot suma 1 que corresponde a la probabilidad de encontrar el 100% de nuestras observaciones.
El paquete {ggplot2}, nos permite realizar varios tipos de visualizaciones debido a la gran variedad de objetos geom. Como ya hemos revisado nuestro conjunto de datos “penguins”, y hemos identificado variables continuas como “bill_length_mm” (longitud del pico en milímetros) y “bill_depth_mm” (profundidad del pico en milímetros). A continuación realizaremos un gráfico de puntos (seleccionado a través del objeto geom_point), donde mapearemos dos variables (es decir, x e y) y no sólo una (es decir, x) como en el ejemplo anterior. Para ello, asignaremos bill_length_mm al eje x, y bill_depth_mm al eje y.
Scatterplot
ggplot(data = penguins,
mapping = aes(x = bill_length_mm,
y = bill_depth_mm)) +
geom_point()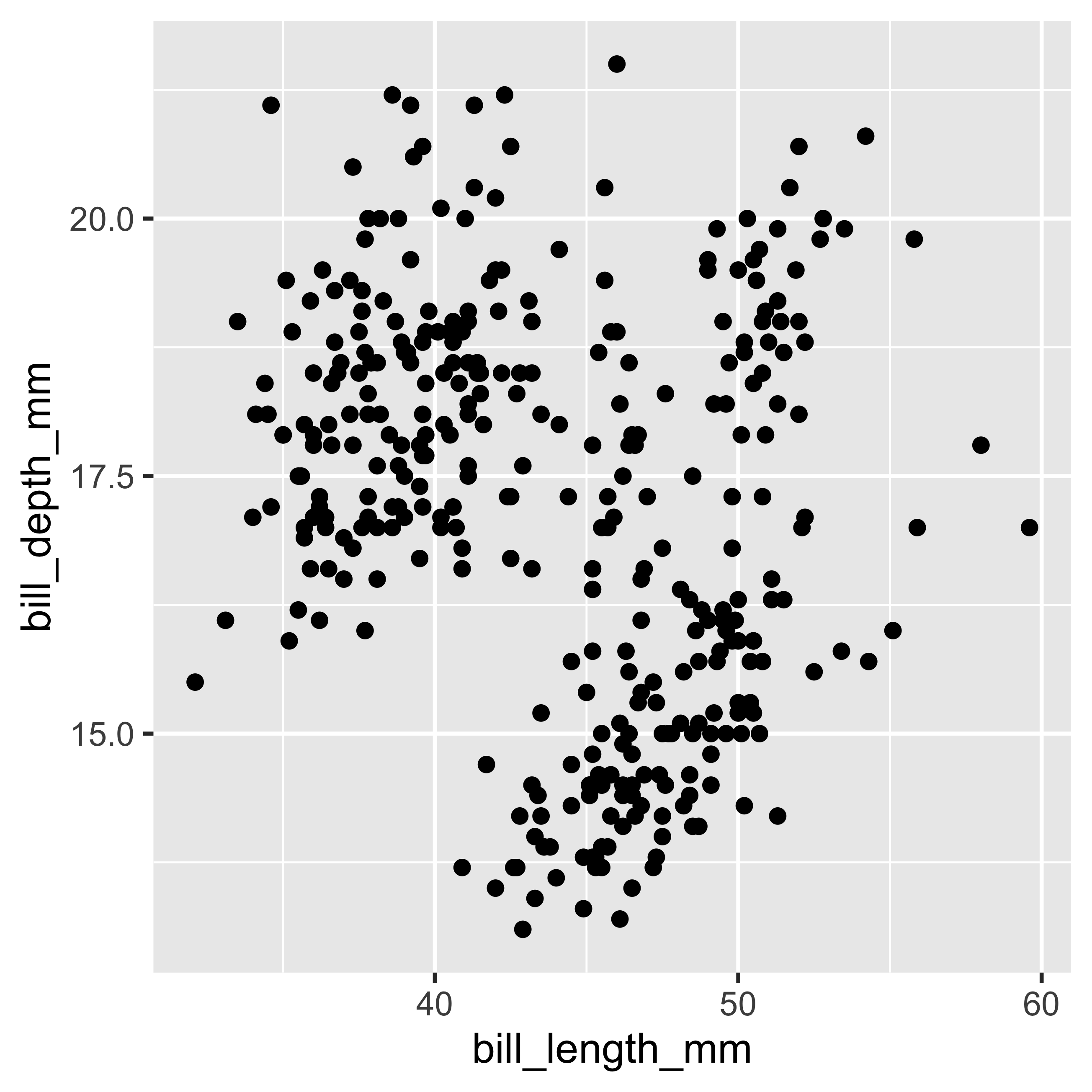
Componentes de un gráfico en {ggplot2}
ggplot(): Es la función que crea un sistema de coordenadas -de forma general, es decir, para todas las capas incorporadas posteriormente- que se incorporarán en las capas. El primer argumento de la función es el conjunto de datos (data =). Por sí misma esta función no genera una capa, pero proporciona toda la información necesaria para añadir una.data: El conjunto de datos (en este caso los penguins) es una colección rectangular de datos con las variables (columnas) y sus observaciones/valores (filas) que hay que mapear.mapping (
aes()) : Aquí se especifica el conjunto de variables y observaciones que se “mapean” o asignan a las propiedades visuales que se utilizarán en el gráfico y qué ejes se asignan a estos valores (x = bill_length_mm,y = bill_depth_mm). Si no se especifican -en general-, deben indicarse en cada capa añadida al gráfico.geom_point() : Las capas del gráfico son incorporadas por las funciones Geom. En este caso, la función añade una capa de puntos al gráfico (scatterplot). ggplot2 incluye más de 30 funciones geom, además de las desarrolladas por otros autores.
Elegir los Colores
El gráfico anterior sólo permite ver la relación entre dos variables numéricas continuas. Sin embargo, el conjunto de datos también tiene información asignada a grupos discretos como especie y el sexo del pingüino. Por este motivo utilizaremos otra propiedad visual como es el color para incorporar una nueva capa de información en el gráfico. Para ello utilizaremos el argumento color dentro de las variables mapeadas en aes(...).
ggplot(data = penguins,
mapping = aes(x = bill_length_mm,
y = bill_depth_mm,
color = species)) +
geom_point()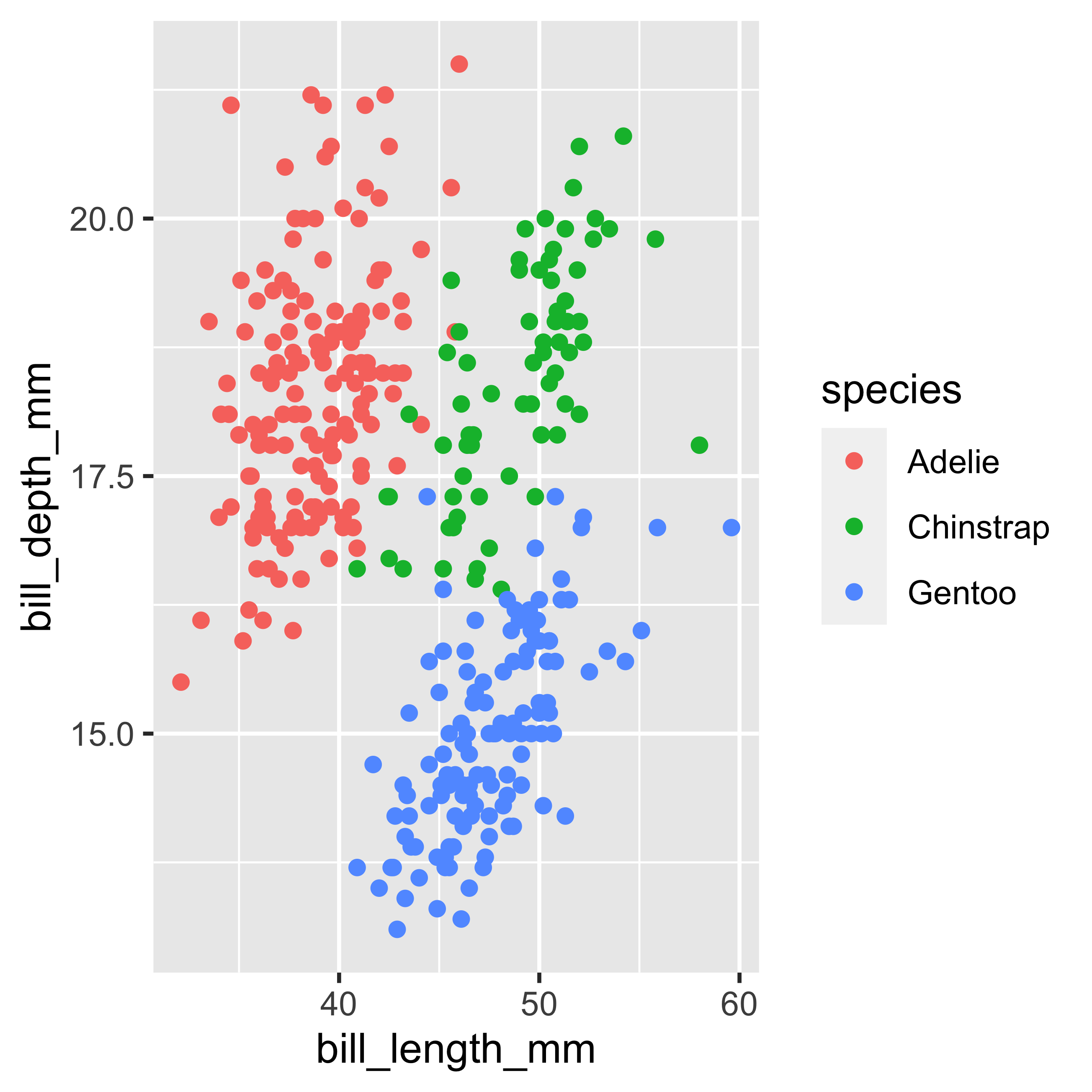
Elija el gráfico con los objeto geom
Una capa en ggplot2, combina datos, propiedades visuales, objetos geométricos (Geoms), funciones estadísticas y/o transformaciones (Stat), y ajuste de posición. En nuestros gráficos anteriores hemos hecho un gráfico de densidad o densiplot y un gráfico de puntos o scatterplot. Por defecto en R hay que elegir un objeto geom_... para generar una visualización, de lo contrario obtendremos una representación sin nuestros datos en ella.
En el gráfico anterior podemos ver que hay diferencias en la distribución de los datos según las especies. Ahora elegiremos otra representación para mostrar mejor la distribución de la variable continua bill_length_mm en función de los grupos discretos presentes (especies) en el conjunto de datos. Para ello cambiaremos nuestro geom de geom_point() a geom_boxplot() y geom_violin().
Boxplot
ggplot(data = penguins,
mapping = aes(x = species,
y = bill_length_mm,
color = species)) +
geom_boxplot()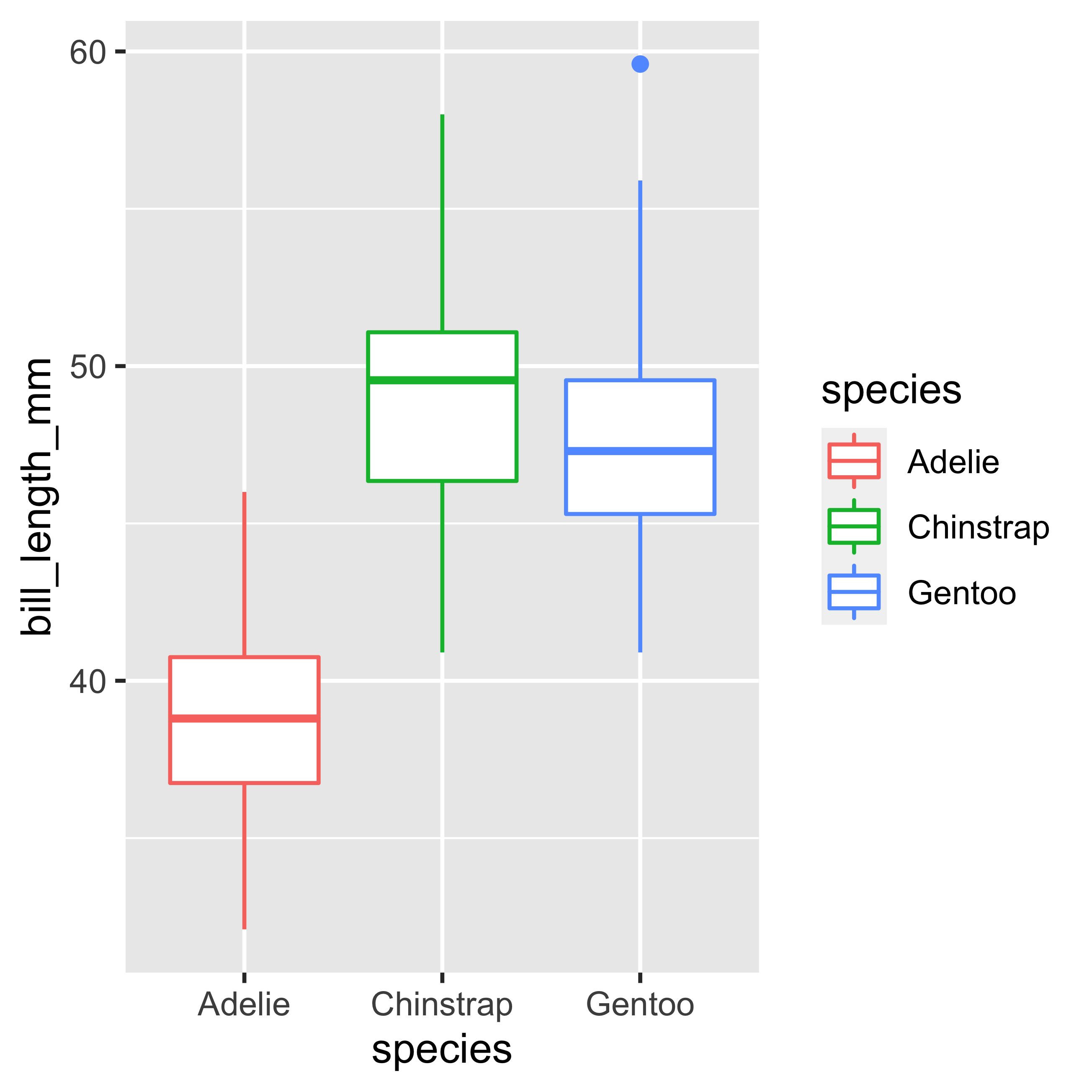
El boxplot es un tipo de visualización muy útil porque nos permite identificar en un solo gráfico los cuantiles (0,25 (Q1), 0,5 (Q2) y 0,75 (Q3)), así como los valores atípicos (outliers) de un conjunto de datos.
¿Cómo interpretar un boxplot?
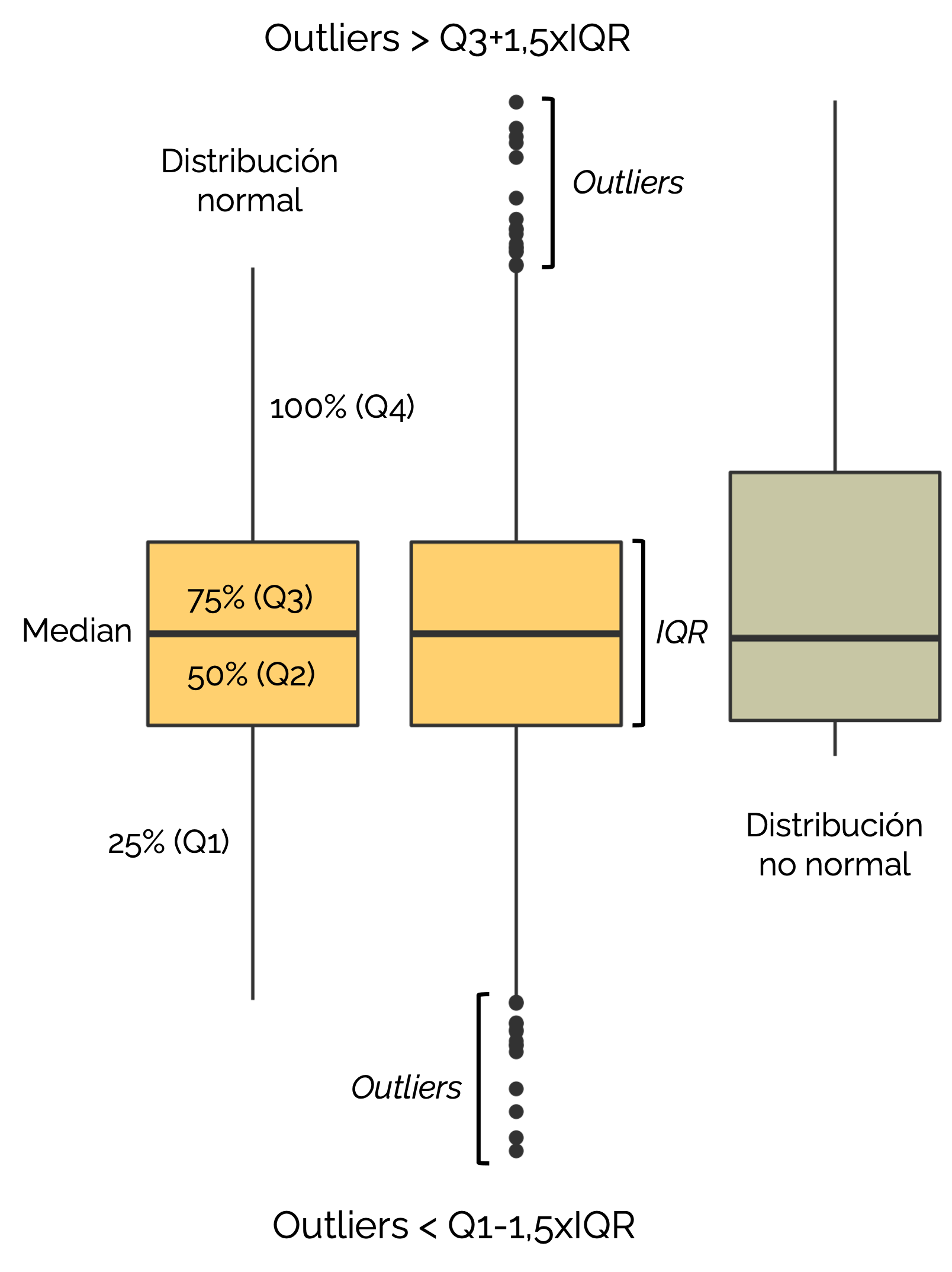
Violin Plot
ggplot(data = penguins,
mapping = aes(x = species,
y = bill_length_mm,
color = species)) +
geom_violin()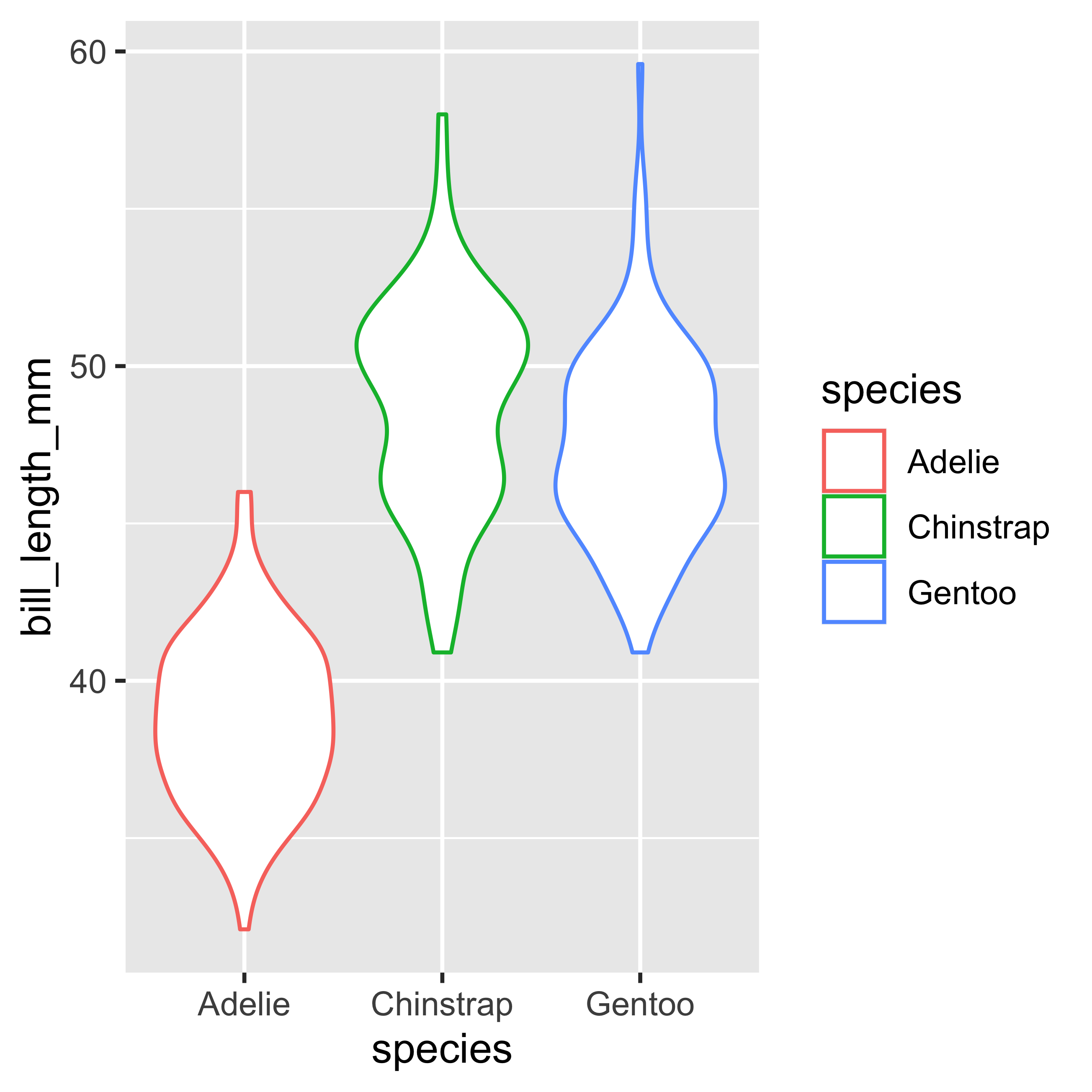
El violin plot es otro tipo de visualización, en el que podemos observar la distribución de los datos, lo que nos permite observar la densidad con mayor claridad.
Complementa tus análisis con {ggpubr}
{ggpubr} es un paquete de R destinado a complementar la visualización de datos con {ggplot2}. {ggpubr} proporciona funciones fáciles de usar que permiten crear y personalizar los gráficos de {ggplot2} y dejarlos listos para su publicación.
Entonces, si aún no hemos instalado {ggpubr}, lo que tenemos que hacer en RStudio es instalar y cargar la librería {ggpubr} con el siguiente código:
# Instalar desde CRAN
install.packages("ggpubr")
# Cargar la librería
library(ggpubr)Funciones de {ggpubr}
Una función útil de {ggpubr} es stat_overlay_normal_density() que nos permite trazar una distribución normal de referencia (basada en nuestros datos) y compararla con la distribución de nuestra variable de interés.
Distribución Normal
ggplot(data = penguins,
mapping = aes(x = bill_length_mm)) +
geom_density() +
stat_overlay_normal_density(color = "darkblue", linetype = "dashed")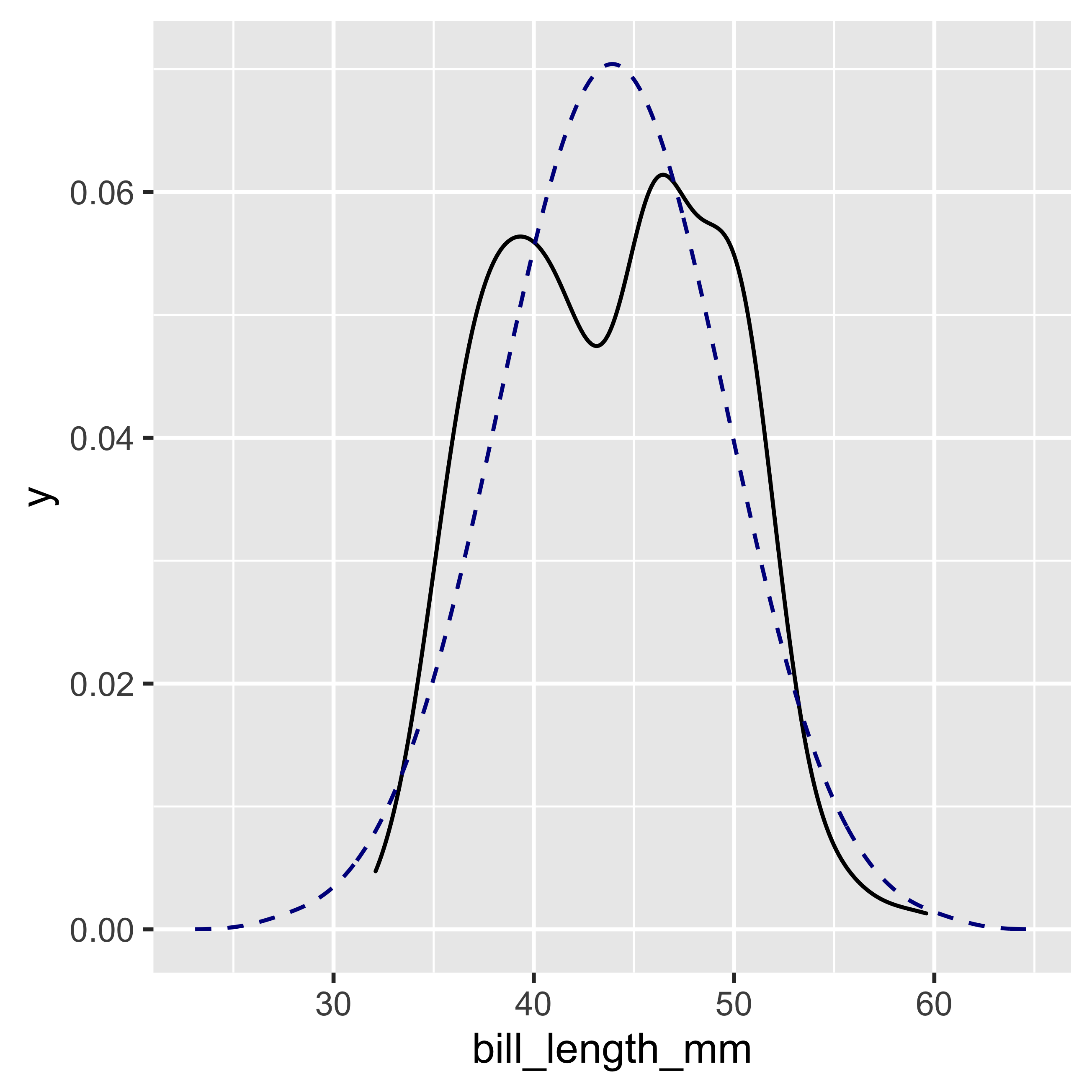
Con esta función podemos ver que nuestra distribución no es perfectamente normal, lo que verifica visualmente el resultado obtenido anteriormente con la prueba de Shapiro-Wilk.
Graficar un análisis de varianza
La siguiente función stat_compare_means() nos permitirá realizar un análisis de varianza con la prueba de Kruskal-Wallis en nuestro boxplot. La segunda comparación incluye la prueba de suma de rangos post-hoc de Wilcoxon, de la misma manera que realizamos el ejemplo anterior con la prueba de Kruskal-Wallis. Por defecto, la función stat_compare_means() calcula la prueba de Kruskal-Wallis cuando hay 3 o más grupos. El argumento ref.group = ".all." se refiere a una comparación de todos los grupos contra todos los grupos. El argumento label.y especifica dónde (con respecto al eje y) se colocarán nuestras leyendas en el gráfico.
ggplot(data = penguins,
mapping = aes(x = species,
y = bill_length_mm,
color = species)) +
geom_boxplot() +
stat_compare_means() +
stat_compare_means(aes(label = ..p.signif..),
method = "wilcox.test",
ref.group = ".all.",
label.y = 65)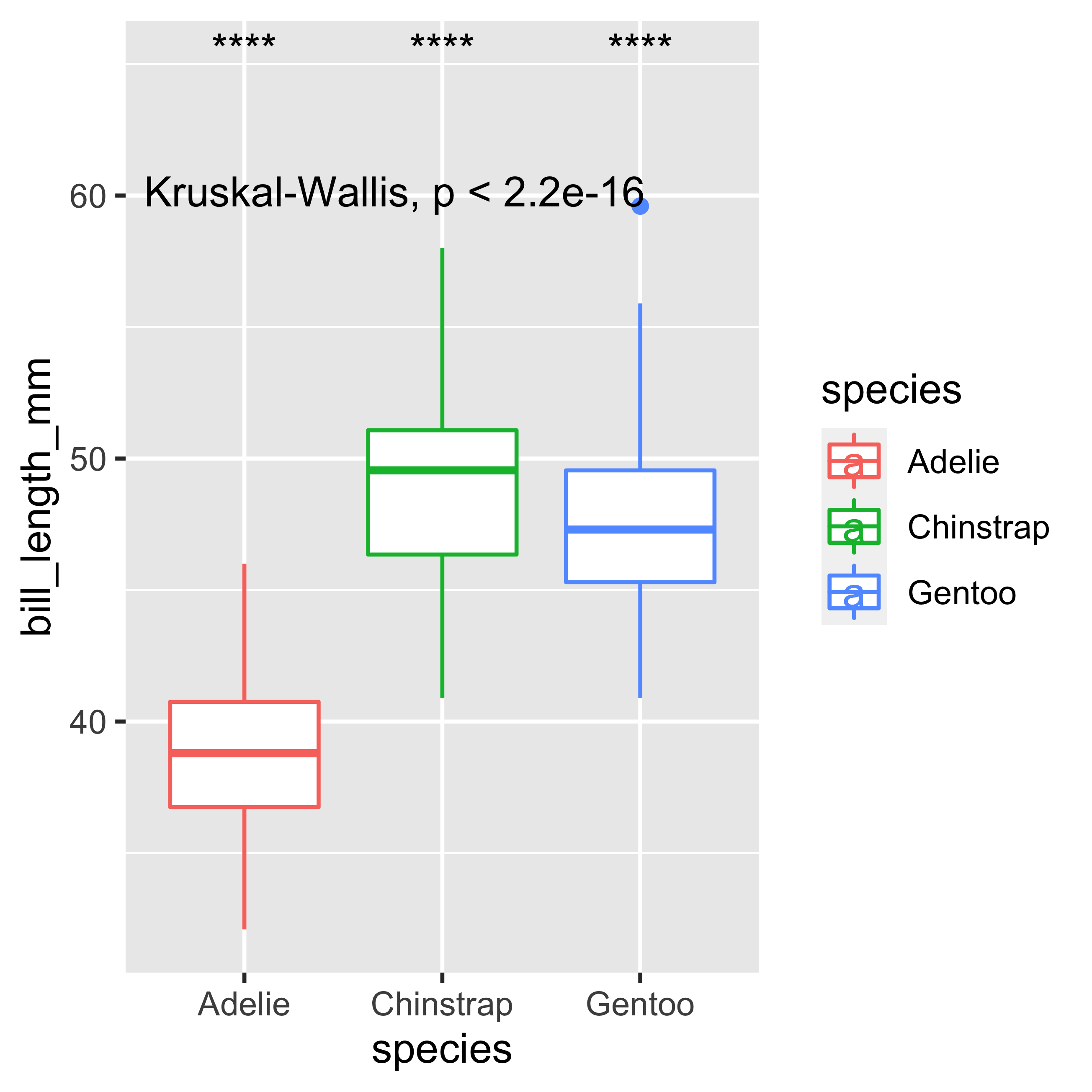
Si queremos realizar la prueba ANOVA debemos seguir el siguiente código, donde se realizará la prueba t pareada. Pero recordemos que en este caso nuestros datos no cumplen con la normalidad, por lo que este ejemplo es sólo una demostración del código.
ggplot(data = penguins,
mapping = aes(x = species,
y = bill_length_mm,
color = species)) +
geom_boxplot() +
stat_compare_means(method = "anova") +
stat_compare_means(aes(label = ..p.signif..),
method = "t.test",
ref.group = ".all.",
label.y = 65)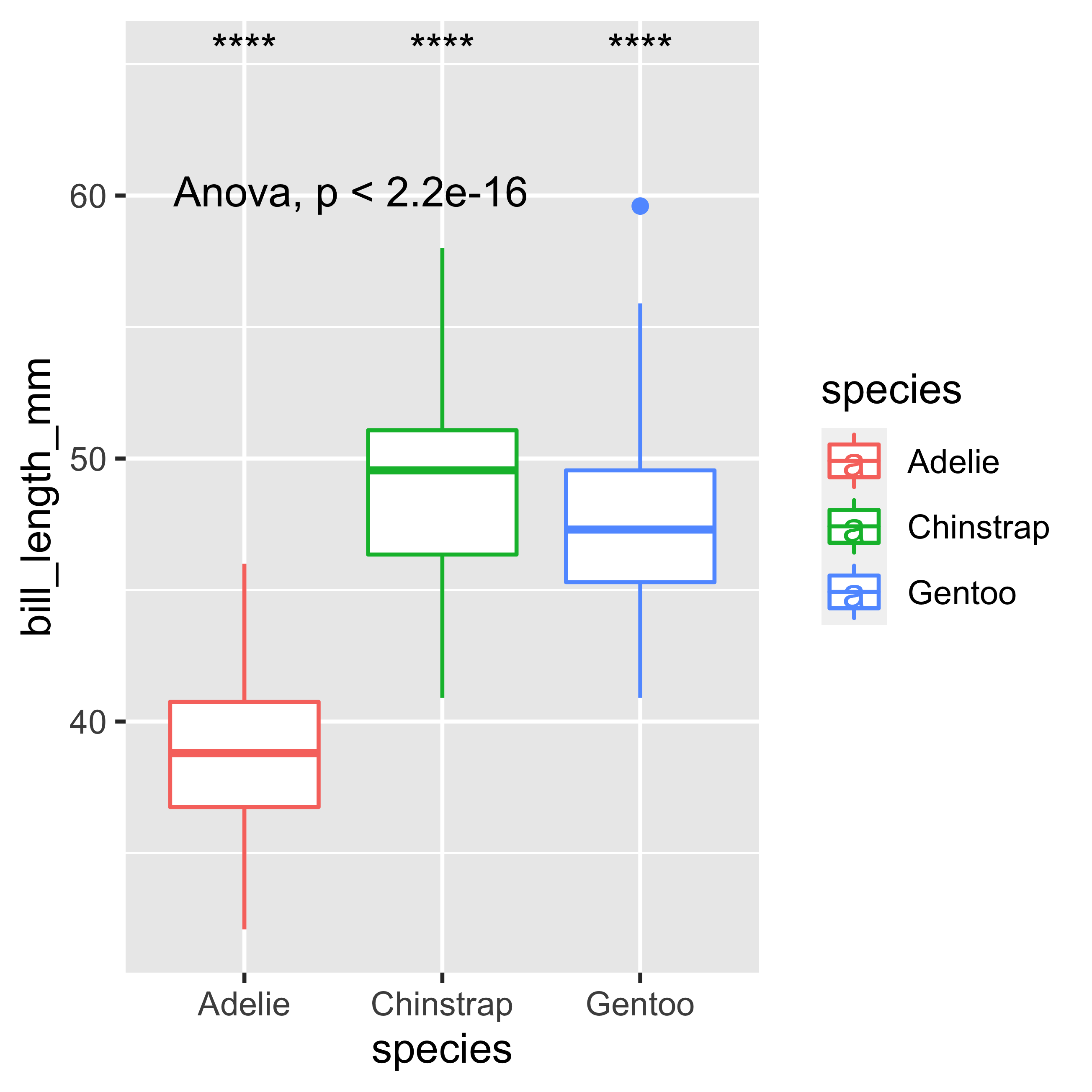
Gráfico final
Ahora que tenemos los resultados de las variables que nos interesan, podemos centrarnos en mejorar los parámetros estéticos de nuestras visualizaciones. Estas modificaciones pretenden que nuestra visualización tenga un aspecto más atractivo y profesional para nuestro futuro público. Debido a la construcción de geom_boxplot(), cuando asignamos el argumento color, éste sólo se representará en el contorno de la figura, por lo que sustituiremos el argumento color por fill, con este simple cambio veremos una mejora inmediata. Además, modificaremos los colores utilizados para representar cada uno de nuestros tres grupos. Para ello utilizaremos la capa scale_fill_manual(), y asignaremos una lista -construida con la siguiente sintaxis c(…)- de tres colores con sus códigos hexadecimales (“#393459”, “#F2AB27”, “#D96704”) al argumento values de la función scale_fill_manual().
ggplot(data = penguins,
mapping = aes(x = species,
y = bill_length_mm,
fill = species)) +
geom_boxplot() +
stat_compare_means() +
stat_compare_means(aes(label = ..p.signif..),
method = "wilcox.test",
ref.group = ".all.",
label.y = 65) +
scale_fill_manual(values = c("#393459","#F2AB27","#D96704"))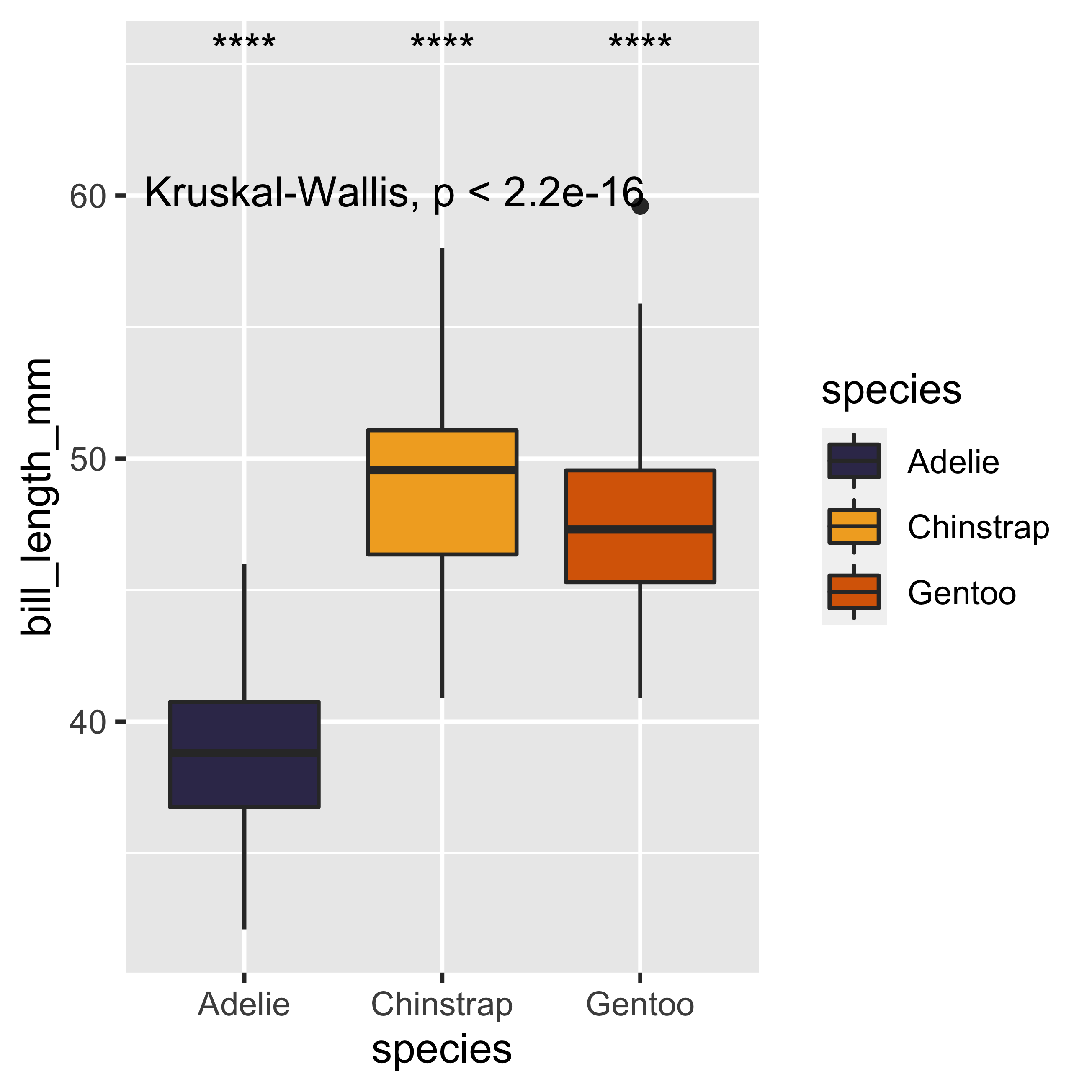
Por último, añadiremos leyendas a cada eje y un título al gráfico, lo que nos ayudará a que la figura sea más autoexplicativa. Para ello utilizaremos la capa labs() y cambiaremos el tema del gráfico por defecto. Cambiar el tema del gráfico es como cambiar el lienzo en el que representamos nuestros datos. Para ello utilizaremos la función theme_pubr(), un tema que está en la librería {ggpubr}, que nos dará un gráfico limpio y elegante, listo para su publicación. Con la adición de estos últimos puntos, nuestro gráfico básico incorpora ahora un análisis estadístico de varianza (prueba de Kruskal-Wallis, y prueba de suma de rangos de Wilcoxon), y un componente estético que lo hará visualmente más atractivo y fácil de interpretar. Además, también puedes crear tu propio tema con la función theme(), pero tendremos que revisarlo con más detalle en un próximo post. ¡Por ahora me despido y espero que tengas un buen día!
# Gráfico básico
ggplot(data = penguins,
mapping = aes(x = species,
y = bill_length_mm,
fill = species)) +
geom_boxplot() +
# Análisis estadístico de varianza
stat_compare_means() +
stat_compare_means(aes(label = ..p.signif..),
method = "wilcox.test",
ref.group = ".all.",
label.y = 65) +
# Paramétros Estéticos
scale_fill_manual(values = c("#393459","#F2AB27","#D96704")) +
labs(x = "Especies de pinguinos",
y = "Longitud del pico (mm)",
fill = "",
title = "Pinguinos del archipelago Palmer,\nAntártica") +
theme_pubr()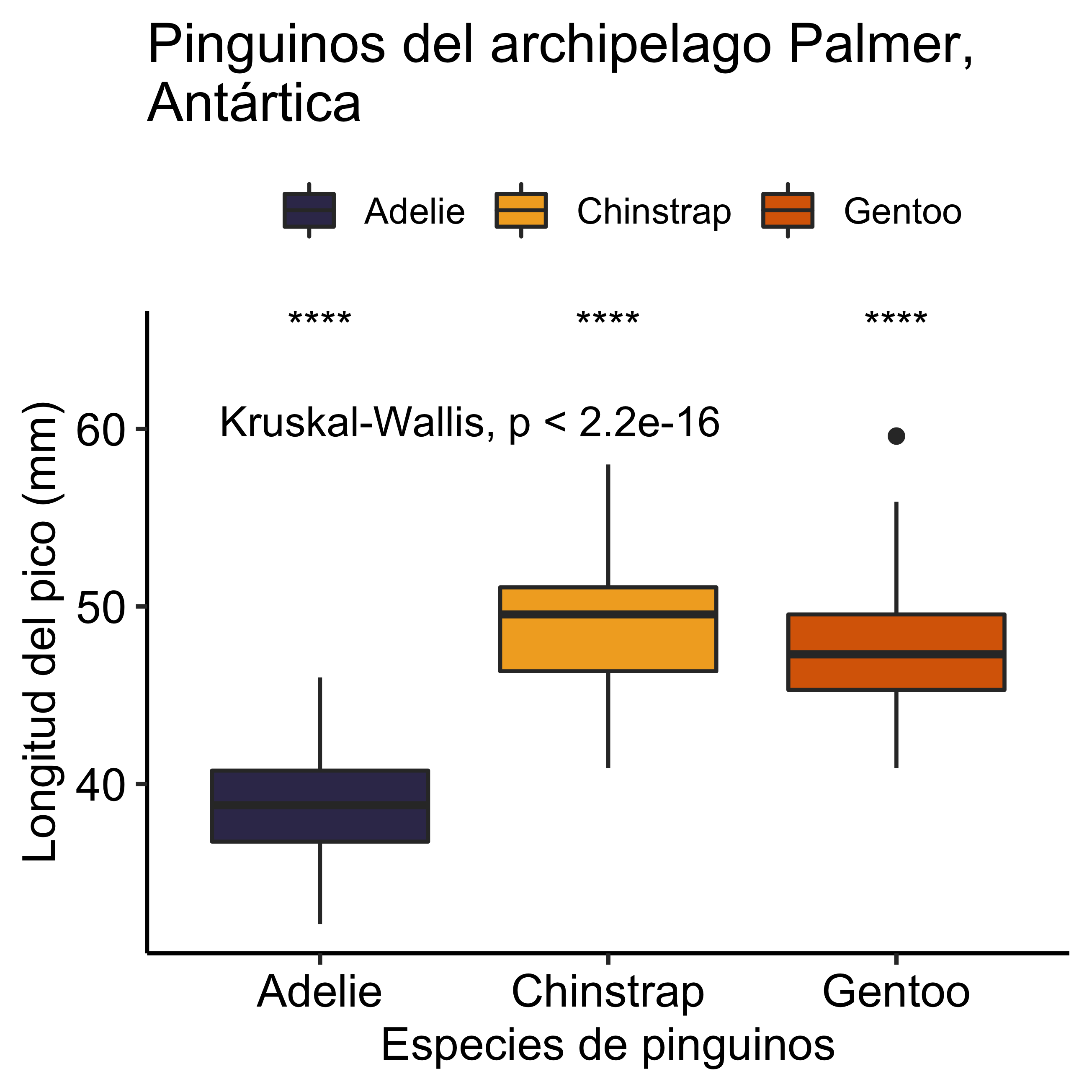
R Session Info
## R version 4.1.3 (2022-03-10)
## Platform: x86_64-apple-darwin17.0 (64-bit)
## Running under: macOS Big Sur/Monterey 10.16
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] forcats_0.5.1 stringr_1.4.0 dplyr_1.0.9 purrr_0.3.4
## [5] readr_2.1.2 tidyr_1.2.0 tibble_3.1.7 tidyverse_1.3.1
## [9] ggpubr_0.4.0 ggplot2_3.3.6 systemfonts_1.0.4
##
## loaded via a namespace (and not attached):
## [1] httr_1.4.3 sass_0.4.1 bit64_4.0.5 vroom_1.5.7
## [5] jsonlite_1.8.0 carData_3.0-5 modelr_0.1.8 bslib_0.3.1
## [9] assertthat_0.2.1 highr_0.9 cellranger_1.1.0 yaml_2.3.5
## [13] pillar_1.7.0 backports_1.4.1 glue_1.6.2 digest_0.6.29
## [17] ggsignif_0.6.3 rvest_1.0.2 colorspace_2.0-3 htmltools_0.5.2
## [21] pkgconfig_2.0.3 broom_0.7.12 haven_2.4.3 bookdown_0.24
## [25] scales_1.2.0 tzdb_0.3.0 generics_0.1.2 farver_2.1.0
## [29] car_3.0-12 ellipsis_0.3.2 DT_0.23 withr_2.5.0
## [33] cli_3.3.0 magrittr_2.0.3 crayon_1.5.1 readxl_1.3.1
## [37] evaluate_0.14 fs_1.5.2 fansi_1.0.3 rstatix_0.7.0
## [41] xml2_1.3.3 blogdown_1.8 tools_4.1.3 hms_1.1.1
## [45] lifecycle_1.0.1 munsell_0.5.0 reprex_2.0.1 compiler_4.1.3
## [49] jquerylib_0.1.4 rlang_1.0.2 grid_4.1.3 rstudioapi_0.13
## [53] htmlwidgets_1.5.4 crosstalk_1.2.0 labeling_0.4.2 rmarkdown_2.11
## [57] gtable_0.3.0 abind_1.4-5 DBI_1.1.2 curl_4.3.2
## [61] R6_2.5.1 lubridate_1.8.0 knitr_1.37 fastmap_1.1.0
## [65] bit_4.0.4 utf8_1.2.2 stringi_1.7.6 parallel_4.1.3
## [69] Rcpp_1.0.8.3 vctrs_0.4.1 dbplyr_2.1.1 tidyselect_1.1.2
## [73] xfun_0.29